归并排序

一、概念及其介绍

归并排序（Merge sort）是建立在归并操作上的一种有效、稳定的排序算法，该算法是采用分治法(Divide and Conquer）的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为二路归并。

二、适用说明

当有 n 个记录时，需进行 logn 轮归并排序，每一轮归并，其比较次数不超过 n，元素移动次数都是 n，因此，归并排序的时间复杂度为 O(nlogn)。归并排序时需要和待排序记录个数相等的存储空间，所以空间复杂度为 O(n)。

归并排序适用于数据量大，并且对稳定性有要求的场景。

三、过程图示

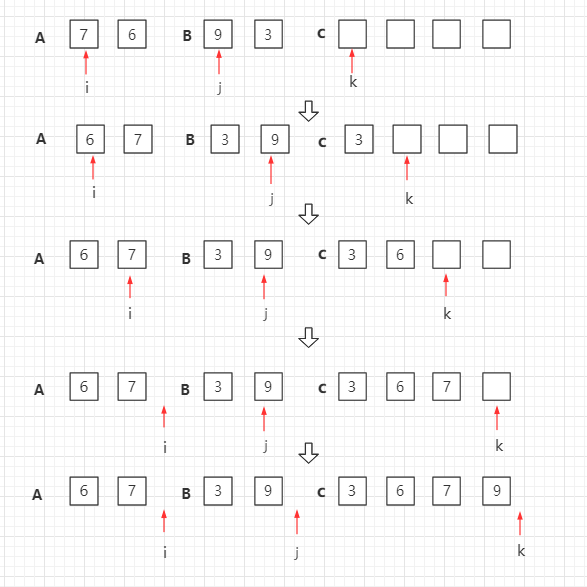
归并排序是递归算法的一个实例，这个算法中基本的操作是合并两个已排序的数组，取两个输入数组 A 和 B，一个输出数组 C，以及三个计数器 i、j、k，它们初始位置置于对应数组的开始端。

A[i] 和 B[j] 中较小者拷贝到 C 中的下一个位置，相关计数器向前推进一步。

当两个输入数组有一个用完时候，则将另外一个数组中剩余部分拷贝到 C 中。

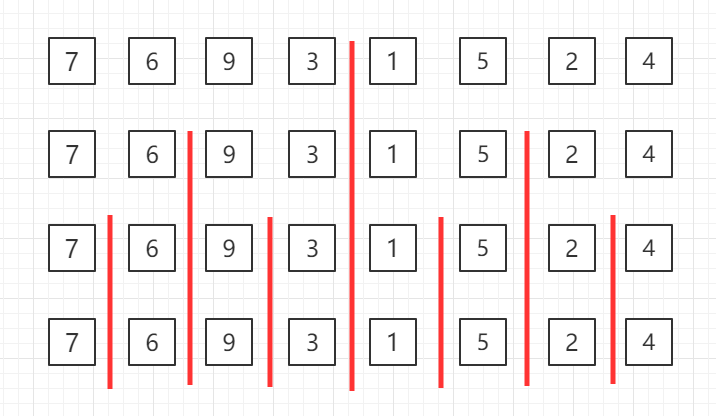
自顶向下的归并排序，递归分组图示：

对第三行两个一组的数据进行归并排序

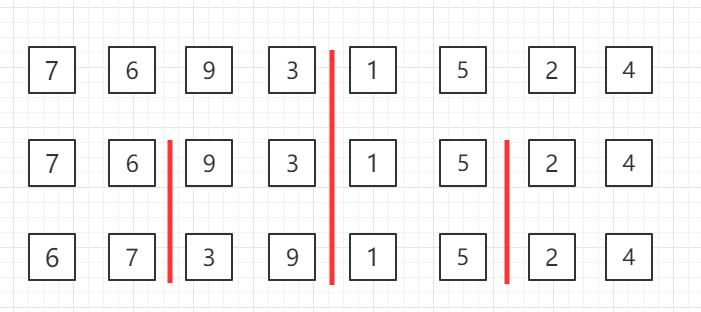
对第二行四个一组的数据进行归并排序

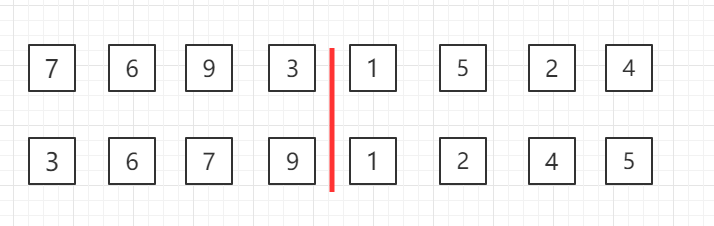
整体进行归并排序

四、Java 实例代码

源码包下载：Download

MergeSort.java 文件代码：

public class MergeSort {

    // 将arr[l...mid]和arr[mid+1...r]两部分进行归并
    private static void merge(Comparable[] arr, int l, int mid, int r) {

        Comparable[] aux = Arrays.copyOfRange(arr, l, r + 1);

        // 初始化，i指向左半部分的起始索引位置l；j指向右半部分起始索引位置mid+1
        int i = l, j = mid + 1;
        for (int k = l; k <= r; k++) {

            if (i > mid) {  // 如果左半部分元素已经全部处理完毕
                arr[k] = aux[j - l];
                j++;
            } else if (j > r) {   // 如果右半部分元素已经全部处理完毕
                arr[k] = aux[i - l];
                i++;
            } else if (aux[i - l].compareTo(aux[j - l]) < 0) {  // 左半部分所指元素 < 右半部分所指元素
                arr[k] = aux[i - l];
                i++;
            } else {  // 左半部分所指元素 >= 右半部分所指元素
                arr[k] = aux[j - l];
                j++;
            }
        }
    }

    // 递归使用归并排序,对arr[l...r]的范围进行排序
    private static void sort(Comparable[] arr, int l, int r) {
        if (l >= r) {
            return;
        }
        int mid = (l + r) / 2;
        sort(arr, l, mid);
        sort(arr, mid + 1, r);
        // 对于arr[mid] <= arr[mid+1]的情况,不进行merge
        // 对于近乎有序的数组非常有效,但是对于一般情况,有一定的性能损失
        if (arr[mid].compareTo(arr[mid + 1]) > 0)
            merge(arr, l, mid, r);
    }

    public static void sort(Comparable[] arr) {

        int n = arr.length;
        sort(arr, 0, n - 1);
    }

    // 测试MergeSort
    public static void main(String[] args) {

        int N = 1000;
        Integer[] arr = SortTestHelper.generateRandomArray(N, 0, 100000);
        sort(arr);
        //打印数组
        SortTestHelper.printArray(arr);
    }
}