有三个立柱A、B、C。A柱上穿有大小不等的圆盘N个,较大的圆盘在下,较小的圆盘在上。要求把A柱上的圆盘全部移到C柱上,保持大盘在下、小盘在上的规律(可借助B柱)。每次移动只能把一个柱子最上面的圆盘移到另一个柱子的最上面。请输出移动过程。
解答
这是动态规划问题中的一种,用递归来实现较为简单方便。
对于"将moveSum个圆盘从from柱移动到to柱(借助by柱)"这个问题,我们可以通过以下三步实现:
- 将from柱最上面的moveSum-1个圆盘移动到by柱(借助to柱)
- 将from柱上剩下的那1个圆盘直接移动到to柱
- 将by柱上的moveSum-1个圆盘移动到to柱(借助from柱)


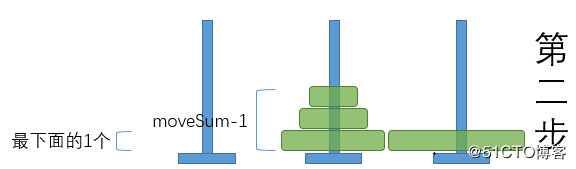
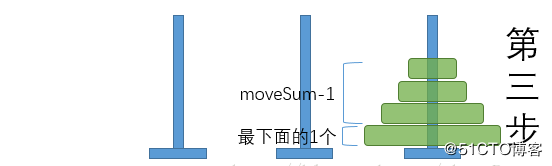
执行的流程如下:


原文链接:https://blog.51cto.com/myunix/2399892

hhhhhh
242***9851@qq.com
1. 定义三种移动方式:A2C(n)、B2C(n)、A2B(n),n个A移动到B,和n个A移动到C,和n个A移动到B本质上都是一样的移动方法和步数,只不过借用的临时存放点不一样而已,所以这三种移动方式所需步数都可以用func(n)来表示。
PS:每次最大那块移动到目的后,其实它的存在不再干扰需要移动块的移动,因为都比它小,所以我们思考时可以把到目的的最大块直接踢出也不会影响后续的移动。
2. 现在来看具体情况:n个A移动到C需要哪几个步骤,即求解func(n);
第一步:n-1个A移动到B,用func(n-1)表示;
第二步:A里剩下的最大那个移动到C,即1次移动;
第三步:n-1个B移动到C,还是可以用func(n-1)表示。
3. 结论:func(n) = 2*func(n-1) + 1
4. 边界条件:0个需要移动0次,所以func(0) = 0。
代码:
def func(n): if n == 0: return 0 return 2*func(n-1) + 1hhhhhh
242***9851@qq.com